GPT 5.2 是我们迄今为止最好的科学模型:GPQA 准确率 92.4%,Frontier Math 准确率 40%,ARC-AGI-2 准确率 52.9%,CharXiv(含工具)准确率 89%,HLE(含工具)准确率 45%…… 此外,在研究层面,该模型的可靠性大大提高。它现在能够一次性求解凸优化问题,找到其最优值!
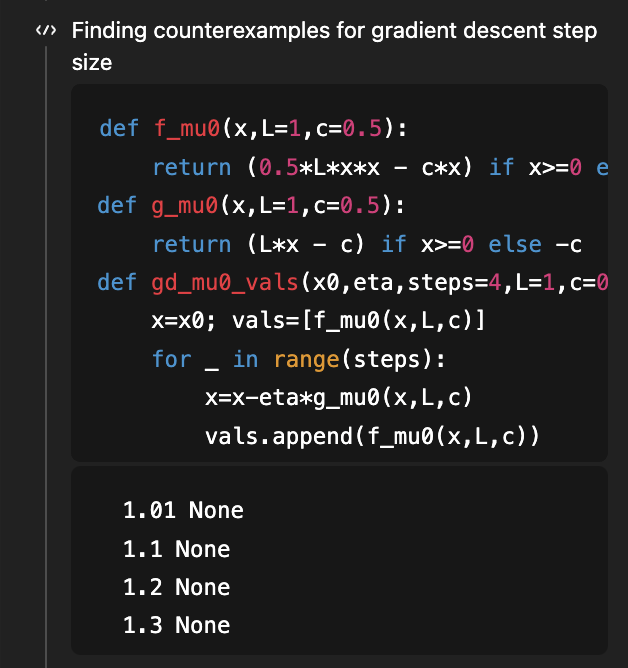
如果你还记得,这是我用来展示 GPT-5 研究能力的第一个问题,目标是确定平滑凸优化梯度下降法的步长条件,使得学习曲线本身也是凸的!有一篇不错的论文表明,η < 1/L 是充分条件,η < 1.75/L 是必要条件。该论文的 v2 版本填补了这一空白,表明 1.75/L 是正确的“当且仅当”条件。 早在八月份(4 个月前!),考虑到论文的 v1 版本,GPT-5 能够将充分条件从 1/L 改进到 1.5/L(距离最优的 1.75/L 还差一些)。 现在,GPT-5.2 在没有任何已知条件的情况下,推导出了 1.75/L 的必要条件和充分条件!为了推导出必要条件,它使用代码搜索反例…… (当然,相应的论文仍然超出了5.2的知识门槛)
这个问题属于理解学习曲线形状这一更广泛的范畴。这类曲线最基本的属性是……它们应该会下降!具体来说,从统计学的角度来看,假设你添加更多数据,你能证明你的测试损失会降低吗? 令人惊讶的是,这一点并不显而易见,而且有很多反例。经典著作[Devroye、Gyorfi、Lugosi,1996]对此进行了详尽的讨论(我记得20年前曾如饥似渴地阅读过这本书,但这又是另一个故事了!)。最近,在2019年的COLT开放问题中,有人指出,一些极其基础的问题版本仍然悬而未决,例如:如果你估计一个未知高斯分布的(协)方差,风险是否单调(即,增加更多数据是否有助于更好地估计该协方差)? @MarkSellke 向 GPT-5.2 提出了这个问题……它居然解决了!之后,Mark 与模型进行了反复的互动,不断推广结果(Mark 除了提出好问题之外,没有提供任何数学输入),而模型也一直在进步……最终,这发展成了一篇优秀的论文,其中包含了正向 KL 分布中高斯分布和伽马分布的结果,以及反向 KL 分布中更一般的指数族的结果。您可以在这里阅读更多内容:https://t.co/XLETMtURcd