从基准测试数据中获取有效信号变得越来越难。我预计在不久的将来,我们不仅会关注平均值,还会关注“argmax”:模型能够提供的最佳输出是什么?毕竟,我们不需要每次都完美解决 PvSNP 问题,一次就足够了😅。因此,考虑到这一点,让我来详细介绍一下我见过的最令人印象深刻的 LLM 输出。
你们中的许多人可能都熟悉优先连接模型(也称为 Barabasi-Albert 模型),这是一个增长的随机图过程,其中每个新节点以与其度成正比的概率连接到现有节点。这与像 X 这样的网络的增长方式非常相似(热门账号会吸引越来越多的粉丝)。 (伊戈尔·科尔切姆斯基制作的精美动图)
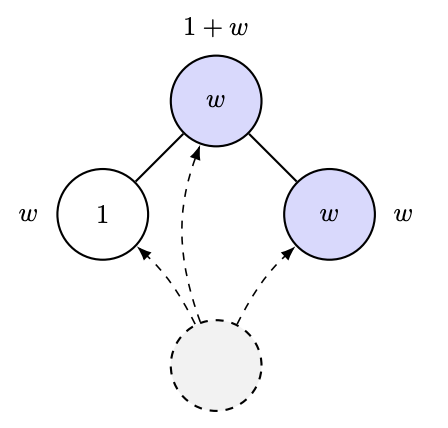
2012年,Ramon和Comendant在他们的COLT开放问题中引入了一种优先连接过程的变体。在这个变体中,每个节点都带有一个“吸引力”参数,其值为1或W>1。现在,节点与前一个节点的连接与其邻居节点的总吸引力成正比!也就是说,如果你有很多有吸引力的朋友,你就会吸引更多的连接。我猜这模拟了人工智能研究实验室的发展过程之类的🤣。他们提出的一个非常简单的问题是:能否通过观察图来估计W?(实际上,他们提出的问题比这更量化,但这正是他们问题的本质。)
人们自然会猜测:或许最热门节点的增长取决于 W 或其他类似因素,也就是度统计量。然而,即便如此,这也相当微妙。Ben-Hamou 和 Velona 最近发表的一篇论文表明,在一个密切相关的模型(均匀连接而非优先连接,且变化基于以更高概率连接到自身吸引力水平)中,度统计量根本无法区分这两种情况!https://t.co/pdwr86OK5A
现在我终于可以宣布我认为迄今为止最令人印象深刻的LLM输出:GPT-5证明了以下定理,该定理给出了上述过程中叶子节点极限比例的封闭形式,进而可以通过观察这样的图来估计W。
该证明(100% 由 GPT-5 完成)出人意料地巧妙,它运用了 Robbins-Monro 型分析(即随机梯度下降法!)来控制关键量的收敛性。此外,在仔细研究证明之前,我们还让 GPT-5 运行了一个模拟程序,并通过实验验证了该公式的合理性……
以前,提出这样的证明、运行模拟等等,我需要花大约一个月的时间。现在,我只用了一个下午就完成了。 感兴趣的读者可以在 https://t.co/IfotVApR3X 的第四章第四节中找到完整的证明和更多细节。 感恩节快乐!