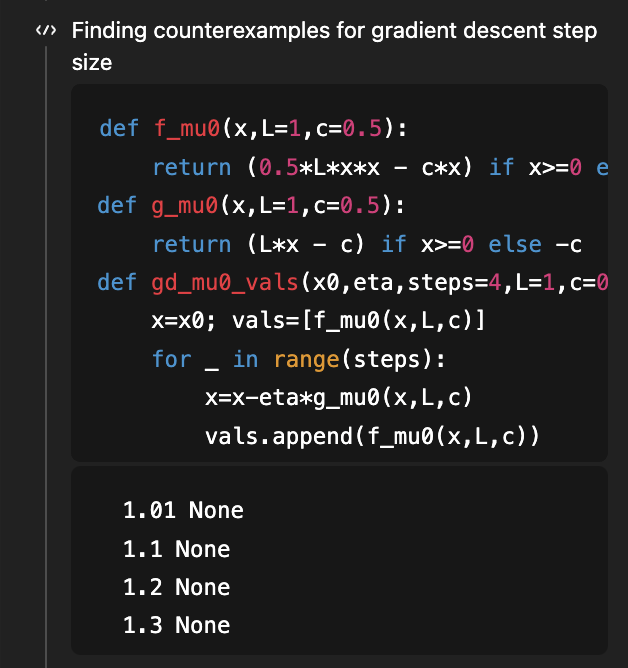
如果你還記得,這是我用來展示 GPT-5 研究能力的第一個問題,目標是確定平滑凸優化梯度下降法的步長條件,使得學習曲線本身也是凸的!有一篇不錯的論文表明,η < 1/L 是充分條件,η < 1.75/L 是必要條件。論文的 v2 版本填補了這一空白,表明 1.75/L 是正確的「當且僅當」條件。 早在八月(4 個月前!),考慮到論文的 v1 版本,GPT-5 能夠將充分條件從 1/L 改進到 1.5/L(距離最優的 1.75/L 還差一些)。 現在,GPT-5.2 在沒有任何已知條件的情況下,推導出了 1.75/L 的必要條件和充分條件!為了推導出必要條件,它使用程式碼搜尋反例… (當然,相應的論文仍然超出了5.2的知識門檻)
這個問題屬於理解學習曲線形狀這個更廣泛的範疇。這類曲線最基本的屬性是…它們應該會下降!具體來說,從統計學的角度來看,假設你添加更多數據,你能證明你的測試損失會降低嗎? 令人驚訝的是,這一點並不顯而易見,而且有許多反例。經典著作[Devroye、Gyorfi、Lugosi,1996]對此進行了詳盡的討論(我記得20年前曾如飢似渴地閱讀過這本書,但這又是另一個故事了!)。最近,在2019年的COLT開放問題中,有人指出,一些極其基礎的問題版本仍然懸而未決,例如:如果你估計一個未知高斯分佈的(協)方差,風險是否單調(即,增加更多數據是否有助於更好地估計該協方差)? @MarkSellke 向 GPT-5.2 提出了這個問題…它居然解決了!之後,Mark 與模型進行了反覆的互動,不斷推廣結果(Mark 除了提出好問題之外,沒有提供任何數學輸入),而模型也一直在進步……最終,這發展成了一篇優秀的論文,其中包含了正向 KL 分佈中高斯分佈和伽馬分佈的結果,以及反向 KL 分佈中更一般的指數族的結果。您可以在這裡閱讀更多內容:https://t.co/XLETMtURcd