從基準測試數據中獲取有效訊號變得越來越困難。我預計在不久的將來,我們不僅會關注平均值,還會關注「argmax」:模型能夠提供的最佳輸出是什麼?畢竟,我們不需要每次都完美解決 PvSNP 問題,一次就夠了😅。因此,考慮到這一點,讓我來詳細介紹我見過的最令人印象深刻的 LLM 輸出。
你們中的許多人可能都熟悉優先連接模型(也稱為 Barabasi-Albert 模型),這是一個增長的隨機圖過程,其中每個新節點以與其度成正比的機率連接到現有節點。這與像 X 這樣的網路的成長方式非常相似(熱門帳號會吸引越來越多的粉絲)。 (伊戈爾·科爾切姆斯基製作的精美動圖)
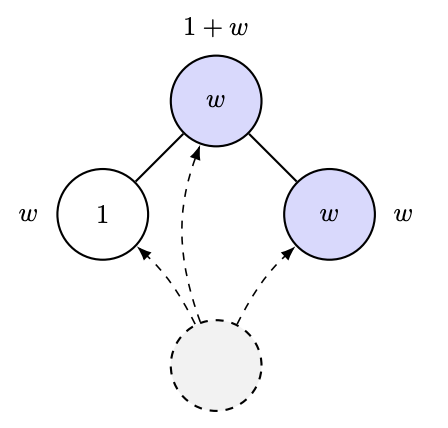
2012年,Ramon和Comendant在他們的COLT開放問題中引入了優先連接過程的變體。在這個變體中,每個節點都帶有一個「吸引力」參數,其值為1或W>1。現在,節點與前一個節點的連接與其鄰居節點的總吸引力成正比!也就是說,如果你有很多有吸引力的朋友,你會吸引更多的連結。我猜這模擬了人工智慧研究實驗室的發展過程之類的🤣。他們提出的一個非常簡單的問題是:能否透過觀察圖來估計W? (實際上,他們提出的問題比這更量化,但這正是他們問題的本質。)
人們自然會猜測:或許最熱門節點的成長取決於 W 或其他類似因素,也就是度統計量。然而,即便如此,這也相當微妙。 Ben-Hamou 和 Velona 最近發表的一篇論文表明,在一個密切相關的模型(均勻連接而非優先連接,且變化基於以更高機率連接到自身吸引力水平)中,度統計量根本無法區分這兩種情況! https://t.co/pdwr86OK5A
現在我終於可以宣布我認為迄今為止最令人印象深刻的LLM輸出:GPT-5證明了以下定理,該定理給出了上述過程中葉子節點極限比例的封閉形式,進而可以通過觀察這樣的圖來估計W。
該證明(100% 由 GPT-5 完成)出乎意料地巧妙,它運用了 Robbins-Monro 型分析(即隨機梯度下降法!)來控制關鍵量的收斂性。此外,在仔細研究證明之前,我們還讓 GPT-5 運行了一個模擬程序,並通過實驗驗證了該公式的合理性…
以前,提出這樣的證明、運行模擬等等,我需要花大約一個月的時間。現在,我只花了一個下午就完成了。 有興趣的讀者可以在 https://t.co/IfotVApR3X 的第四章第四節中找到完整的證明和更多細節。 感恩節快樂!