三年前,我們或許可以用一幅獨角獸圖畫來展示人工智慧的尖端技術。而今天,我們可以用觸及科學前沿的人工智慧成果來做到這一點:https://t.co/ALJvCFsaie 請查閱該文檔,自行判斷人工智慧輔助科學加速的現狀,並希望從中汲取一些靈感!
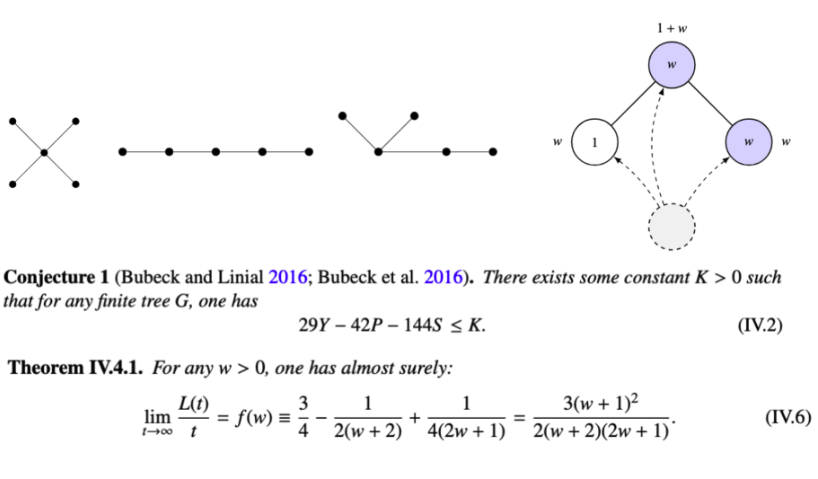
長話短說,我只簡單討論最後兩部分:我們讓一個搭建好的 GPT-5 去解決不到 10 個問題,其中包括我和 Linial 在 2013 年提出的一個猜想,以及一個 COLT 2012 年的未解問題。經過兩天的思考,它竟然給了…2012 年和 2013 年問題的完整解決方案! ! !
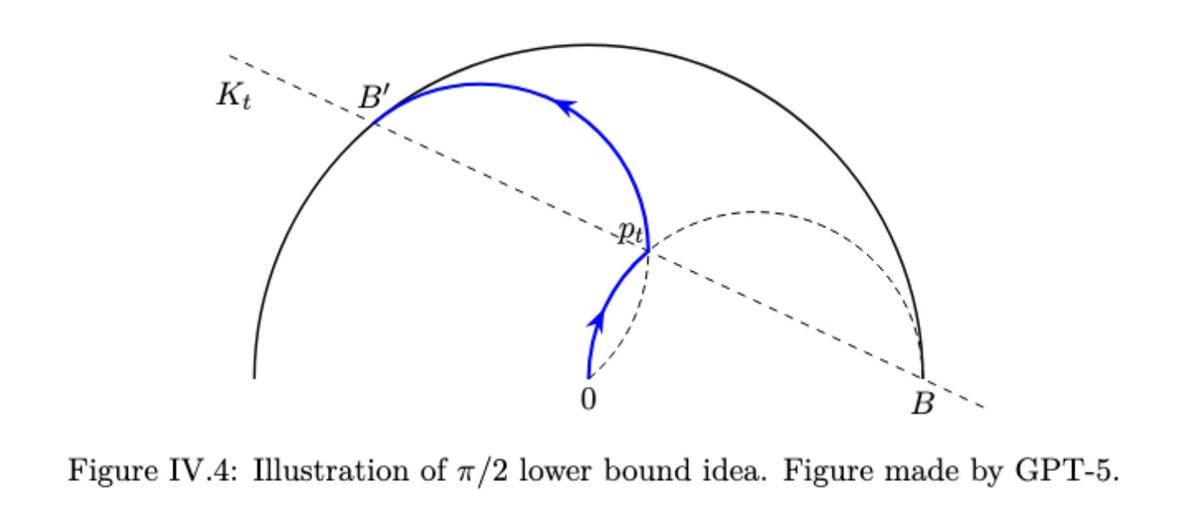
需要說明的是,這些結果的範圍很窄:少數專家可能只花了幾個星期的時間思考這些問題。我們討論的並非黎曼猜想或朗蘭茲綱領!但即便如此,我認為這仍然非常令人印象深刻。順便一提,我們也確實包含了一個針對埃爾德什問題的全新解決方案 :-) (這更像是人工智慧與人類的合作,詳見 Mehtaab Sawhney 和 @MarkSellke 撰寫的 IV.1 節)。 我必須提一下克里斯蒂安·科斯特(Christian Coester)在凸體追蹤問題上取得的另一項非常酷的AI-人類合作成果,這個問題正是我非常感興趣的。他們利用GPT-5證明了π/2是二維凸體追蹤問題的下界(請參閱附件中GPT繪製的精美圖示,了解其建構過程)! 最後,我相信你們中的許多人都會非常喜歡@wtgowers撰寫的關於他如何在研究中使用GPT-5的那部分。它真的非常鼓舞人心。 這篇論文除了數學部分之外,還涉及其他內容。我邀請您查看 @ALupsasca 的帖子以了解物理部分,並查看 @DeryaTR_ 的帖子以了解生物學部分!
看到這裡,你可能會想,GPT-5 是如何做到這一切的? 簡單的: ...
不過說真的,我們知道這篇論文篇幅很長,技術性也很強,但我們認為這種深度對於就人工智慧在科學領域的現狀以及未來的發展方向進行深入探討是必要的。 https://t.co/ALJvCFsaie