ベンチマーク数値からシグナルを得ることはますます難しくなってきています。平均値ではなく、近い将来には「argmax」、つまりモデルが出力できる最良の出力は何かという点も重要になると思います。結局のところ、PvsNPを10回中10回解く必要はなく、1回で十分です😅。そこで、それを念頭に、私が今まで見た中で最も印象的なLLM出力についてもう少しお話ししましょう。
皆さんの多くは、優先的接続モデル(別名バラバシ・アルバート)をご存知でしょう。これは、新しいノードが既存のノードに次数に比例した確率で接続する、成長ランダムグラフプロセスです。これは、Xのようなネットワークの成長過程(人気アカウントがより多くのフォロワーを引き付ける)と非常に似ています。 (Igor Kortchemskiによる美しいGIF)
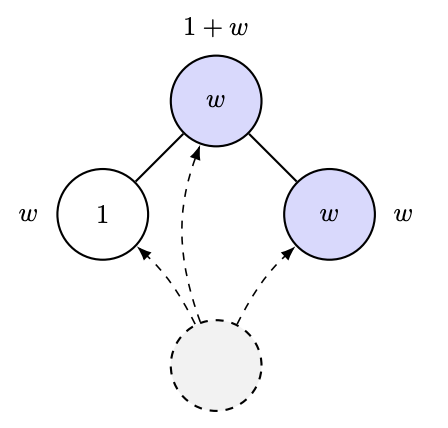
2012年、ラモンとコメンダントはCOLTの未解決問題において、優先的接続過程の変種を導入しました。この過程において、各ノードは「魅力度」パラメータ(1またはW>1)を持って生まれ、前のノードへの接続は隣接するノードの魅力度の合計に比例するようになります。つまり、魅力的な友人がたくさんいれば、より多くの接続を引き寄せるということです。これはAI研究室の成長過程をシミュレートしたものだと思います🤣。彼らが問うた非常にシンプルな問いは、「グラフを観察することでWを推定できるか?」というものでした。[実際にはこれよりも定量的な問いでしたが、それが彼らの問いの本質です。]
当然、次のような推測をしたくなるかもしれません。「最も人気のあるノードの成長は、Wとかそういうもの、つまり次数統計に依存するのではないか」と。まあ、少なくともそれが本当だとしても、これはかなり微妙な問題です。ベン=ハムーとヴェローナによる最近の論文では、密接に関連するモデル(優先的付着ではなく均一付着、そして変動は自身の魅力レベルに高い確率で付着することに基づく)では、次数統計ではその違いを区別できないことが示されています! https://t.co/pdwr86OK5A
私はついに、私が今まで見た中で最も印象的なLLM出力について述べることができます。GPT-5は次の定理を証明しました。これは、上記のプロセスにおける葉の限界割合の閉じた形を与え、それによってそのようなグラフの観測からWを推定することを可能にします。
証明(100% GPT-5)は驚くほど巧妙で、ロビンス・モンロー(つまりSGD!)型の解析を用いて主要な量の収束を制御しています。また、証明を見る前に、GPT-5にシミュレーションを実行させ、式が信頼できるかどうかを経験的に確認しました…
以前は、このような証明を考え出し、シミュレーションを実行し、その全てをこなすのに約1ヶ月かかっていました。今では午後1日で完了します。 興味のある方は、https://t.co/IfotVApR3X の第 4 章、セクション 4 で完全な証明と詳細をご覧いただけます。 感謝祭おめでとうございます!