Deixa eu explicar isso com mais propriedade, como se diz. Acho que muita gente acredita numa versão desse argumento que é exagerada. Mas acho que existem muitas outras versões que são basicamente corretas.
O que significa "gerar conhecimento", digamos, de uma proposição verdadeira, mas desconhecida, P? Creio que significa que existe uma proposição contextual C que elicita do LLM um "argumento" A que é verdadeiro e implica P. Se isso ocorrer, então o conhecimento de P foi gerado.
Portanto, a versão mais obviamente errada do argumento citado é que isso não pode acontecer. Claramente pode, e acontece o tempo todo, geralmente de maneiras triviais. O código que implementa uma funcionalidade para meu aplicativo é desconhecido. Eu pergunto ao LLM. Ele gera o código. Pronto, novo conhecimento.
Dito isso, que comece a análise detalhada. Primeiro, o ponto mais básico. Tudo o que um LLM "sabe" é estático no curto prazo. Ele esquece tudo entre as sessões. Uma vez que deriva A, não "sabe" automaticamente P. Isso parece um pouco diferente do que acontece com as pessoas.
Uma vez que Euclides demonstra I.46: você pode construir um quadrado, I.46 torna-se parte de seu conhecimento, e ele pode aplicá-lo para demonstrar o Teorema de Pitágoras. Uma vez que o LLM demonstra P, P não se torna "parte de seu conhecimento" da mesma maneira.
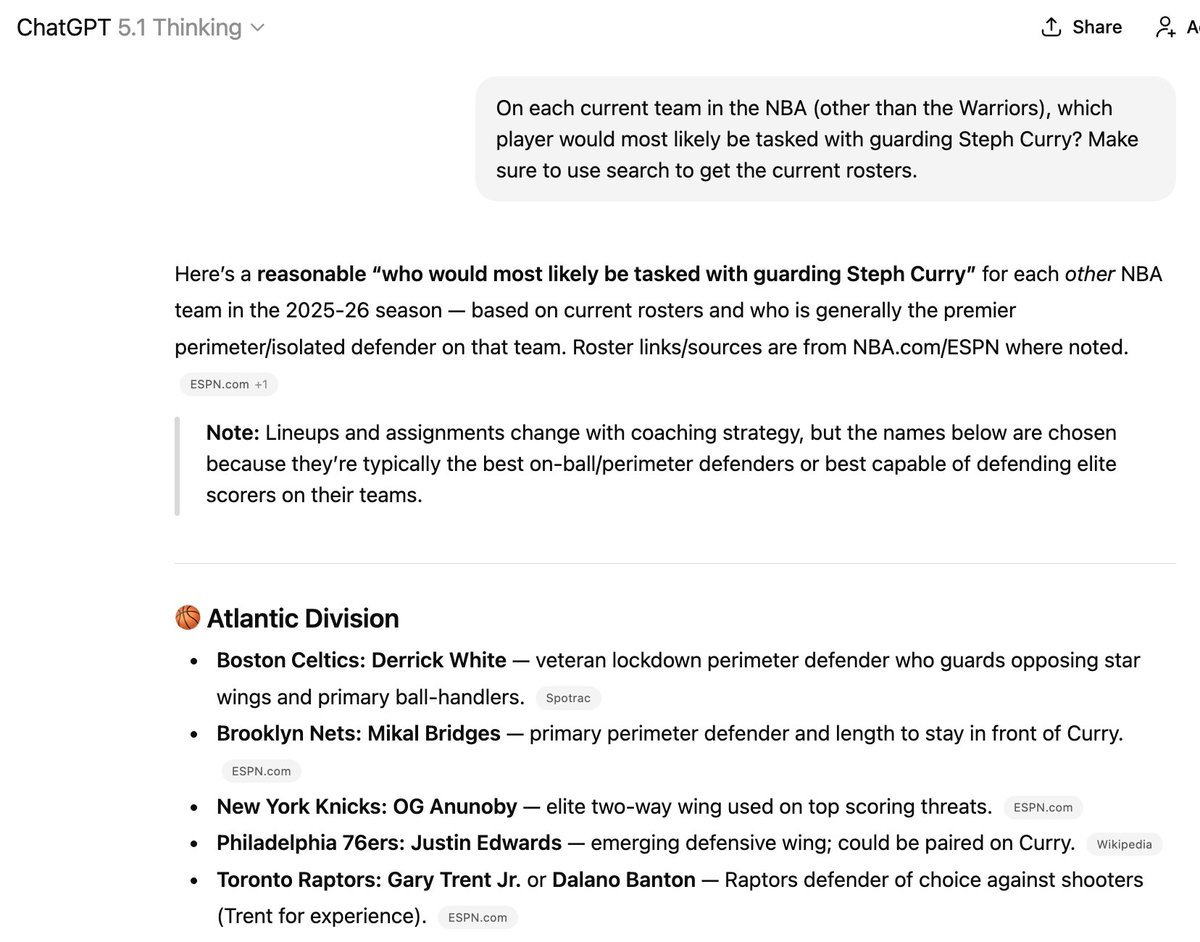
Existem maneiras de tentar inserir P nos dados de treinamento, mas isso ainda é bastante impreciso. É por isso que coisas assim acontecem. Três dos seis jogadores mencionados aqui não estão mais nos times listados, mas é difícil fazer o modelo "aprender" coisas novas!
(Aliás, eu não recomendaria contratar essa coisa para treinar seu time da NBA)
Este ponto concorda com a afirmação de que "só pode misturar informações que já foram encontradas...". Sabe o que sabe. Isso é basicamente estático a curto prazo (ou seja, entre treinamentos) e evolui de forma imprevisível a longo prazo.
Acho que esse ponto é importante para as alegações sobre a cura do câncer e coisas do tipo. Curar o câncer não será como resolver um problema de Putnam. Envolverá acompanhar e conectar novos fatos que ainda não são conhecidos e que podem até contradizer as crenças atuais.
De certa forma, acredito que isso será semelhante a acompanhar qual jogador está atualmente em qual time de basquete, uma tarefa na qual até mesmo os modelos de raciocínio de nível de doutorado mais avançados, com acesso ilimitado à internet, permanecem incapazes até hoje.
Certo, outra abordagem de Steelmann. O LLM não gera A deterministicamente. Ele gera A com alguma probabilidade. Com alguma outra probabilidade, ele pode gerar B (para "argumento ruim"), o que implica ~P. E nós realmente não sabemos quais são essas probabilidades.
O que devo concluir disso? No caso em que produziu a resposta correta, "gerou conhecimento"? Aqui, está misturando, combinando e recombinando vários fragmentos de informação matemática, muito parecido com o descrito no tweet citado que estou analisando em detalhes.
Por diversos meios, alguns manuais e outros automatizados, posso verificar se algum desses argumentos está correto e se suas conclusões são verdadeiras. Ao fazer isso, provavelmente descobrirei argumentos corretos com conclusões verdadeiras que podem ser desconhecidas anteriormente.
Mas, a meu ver, é menos um processo de "geração" autônoma de conhecimento e mais um processo de "extração" de conhecimento. O LLM contém um conjunto de verdades e um conjunto de falsidades. O desafio é extrair as verdades e descartar as falsidades.
Ao contrário de muitos outros entusiastas do LLM, acredito que o preenchimento automático glorificado, com palpites aleatórios sobre o próximo token, seja na verdade a maneira mais correta e útil de pensar sobre essas coisas. Digo isso como um ávido entusiasta do LLM há muito tempo. Acho que muitas pessoas discordam dessa caracterização.
A premissa era que jamais poderíamos aprender algo novo adivinhando aleatoriamente o próximo token. Mas, é claro que podemos! Se você deixar cair um monte de agulhas de igual comprimento em um piso de madeira, poderá contar as interseções para estimar o valor de π. Há muita informação para extrair disso.
processos aleatórios, se você souber como. Mas eu me pergunto o quanto realmente há lá dentro. Talvez a cura para o câncer esteja em algum lugar ali e tudo o que você precisa fazer é fornecer o estímulo certo. Ou talvez haja alguns problemas de Erdős não resolvidos e algumas outras coisas fáceis de descobrir, e só.