O GPT 5.2 é o nosso melhor modelo para ciência até o momento: 92,4% GPQA, 40% Frontier Math, 52,9% ARC-AGI-2, 89% CharXiv (com ferramentas), HLE 45% (com ferramentas) ... Além disso, em nível de pesquisa, o modelo se tornou muito mais confiável. Agora, ele resolve o problema de otimização convexa em uma única tentativa, encontrando o valor ótimo!
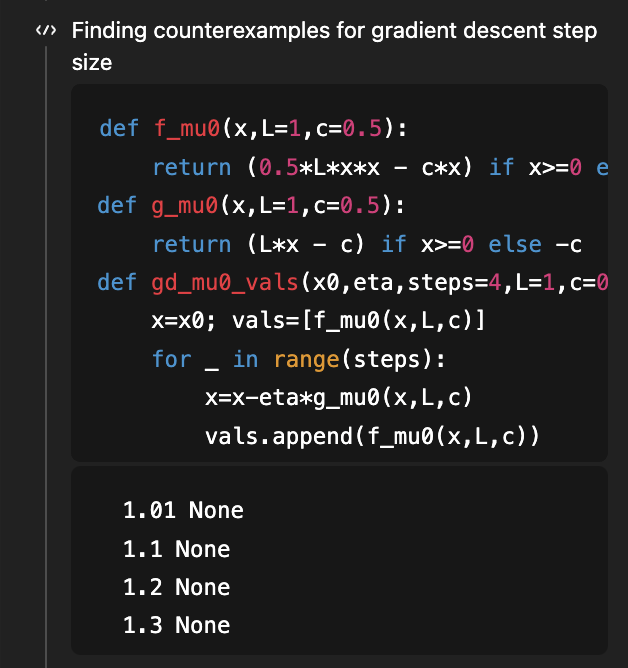
Como você deve se lembrar, este foi o primeiro problema que usei para demonstrar as capacidades de pesquisa do GPT-5, e o objetivo era determinar a condição de tamanho do passo sob a qual o método do gradiente descendente para otimização convexa suave admite uma curva de aprendizado que também seja convexa! Havia um ótimo artigo mostrando que η < 1/L é suficiente e η < 1,75/L é necessário, e uma versão 2 desse artigo corrigiu essa discrepância, mostrando que 1,75/L é a condição correta "se e somente se". Em agosto (há 4 meses!), considerando a versão 1 do artigo em contexto, o GPT-5 conseguiu melhorar a condição suficiente de 1/L para 1,5/L (ficando muito aquém do ideal de 1,75/L). Agora, o GPT-5.2, sem receber NADA, deriva AMBAS as condições necessárias e suficientes de 1,75/L! Para derivar a parte necessária, ele usa código para pesquisar contraexemplos... (e, claro, o artigo correspondente ainda está além do nível de conhecimento exigido de 5.2)
Este problema se encaixa em um contexto mais amplo de compreensão do formato das curvas de aprendizado. A propriedade mais básica dessas curvas é que, idealmente, elas são decrescentes! Especificamente da perspectiva estatística, suponha que você adicione mais dados: você consegue provar que a perda no teste será menor? Surpreendentemente, isso não é nada óbvio e existem muitos contraexemplos. Isso foi discutido extensivamente no livro clássico [Devroye, Gyorfi, Lugosi, 1996] (que me lembro de ter lido vorazmente há 20 anos, mas essa é outra história!). Mais recentemente, em um Problema em Aberto do COLT de 2019, foi apontado que algumas versões extremamente básicas dessa questão ainda estão em aberto, como: se você estima a (co)variância de uma gaussiana desconhecida, o risco é monotônico (ou seja, adicionar mais dados ajuda a estimar melhor essa covariância)? @MarkSellke fez essa pergunta ao GPT-5.2 e... ele a resolveu! Então, Mark interagiu com o modelo para continuar generalizando o resultado (sem nenhuma intervenção matemática da parte dele, exceto por fazer boas perguntas) e o processo continuou... eventualmente, isso se tornou um ótimo artigo, com resultados para distribuições Gaussianas e Gama para o algoritmo de Kullback-Leibler direto, e famílias exponenciais mais gerais para o algoritmo de Kullback-Leibler reverso. Você pode ler mais sobre isso aqui: https://t.co/XLETMtURcd.