Está cada vez mais difícil obter informações relevantes a partir de números de referência. Em vez de médias, acredito que em um futuro próximo também nos preocuparemos com o "argmax": qual é o MELHOR resultado que um modelo pode fornecer? Afinal, não precisamos resolver o problema PvsNP 10 vezes em 10 tentativas, uma vez basta 😅. Então, com isso em mente, deixe-me contar um pouco mais sobre o RESULTADO MAIS IMPRESSIONANTE de um modelo LLM que já vi.
Muitos de vocês provavelmente estão familiarizados com o modelo de ligação preferencial (também conhecido como Barabási-Albert), que é um processo de crescimento em grafos aleatórios, onde cada novo nó se liga a nós existentes com probabilidade proporcional aos seus graus. Isso é muito semelhante a como uma rede como X cresce (contas populares atraem cada vez mais seguidores). (lindo gif de Igor Kortchemski)
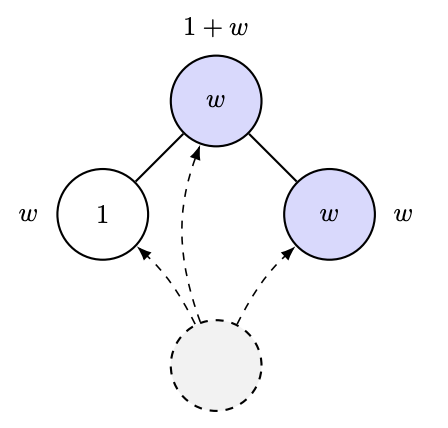
Em 2012, Ramon e Comendant introduziram, em seu problema em aberto COLT, uma variante do processo de ligação preferencial, onde cada nó nasce com um parâmetro de "atratividade", seja 1 ou W>1, e agora a conexão com um nó anterior é proporcional à atratividade total de seus vizinhos! Ou seja, se você tem muitos amigos atraentes, você atrairá mais conexões. Imagino que isso simule como um laboratório de pesquisa em IA cresce ou algo assim 🤣. A pergunta muito simples que eles fizeram foi: é possível estimar W observando o grafo? [Na verdade, eles fizeram uma pergunta mais quantitativa, mas essa é a essência da questão.]
Naturalmente, alguém poderia ser tentado a supor coisas como: "Ei, talvez o crescimento do nó mais popular dependa de W ou algo assim, ou seja, de uma estatística de grau". Bem, no mínimo, se isso fosse verdade, seria bastante delicado, já que um artigo recente de Ben-Hamou e Velona mostra que, em um modelo intimamente relacionado (apego uniforme em vez de apego preferencial, e a variação é baseada na ligação ao seu próprio nível de atratividade com maior probabilidade), as estatísticas de grau NÃO CONSEGUEM distinguir! https://t.co/pdwr86OK5A
Finalmente posso afirmar o que, na minha opinião, é o resultado mais impressionante de um algoritmo de aprendizado de máquina (LLM) que já vi: o GPT-5 provou o seguinte teorema, que fornece uma fórmula fechada para a fração limite de folhas no processo descrito acima, o que, por sua vez, permite estimar W a partir da observação de tal grafo.
A demonstração (100% GPT-5) é surpreendentemente inteligente, usando análise do tipo Robbins-Monro (ou seja, SGD!) para controlar a convergência de quantidades-chave. Além disso, antes de nos darmos ao trabalho de analisar a demonstração, pedimos ao GPT-5 para executar uma simulação e verificar empiricamente se a fórmula era plausível...
Elaborar essa demonstração, executar a simulação e tudo mais, era algo que eu costumava levar cerca de um mês. Agora, isso foi feito em uma tarde. Para os interessados, a prova completa e mais detalhes podem ser encontrados no Capítarxiv.org/abs/2511.16072s://t.co/IfotVApR3X. Feliz Dia de Ação de Graças!