GPT 5.2는 현재까지 우리가 개발한 과학 분야 최고의 모델입니다: GPQA 92.4%, Frontier Math 40%, ARC-AGI-2 52.9%, CharXiv(도구 포함) 89%, HLE(도구 포함) 45% 등의 수치를 기록했습니다. 게다가 연구 수준에서 모델의 신뢰도가 훨씬 높아졌습니다. 이제 볼록 최적화 문제를 단 한 번의 시도로 최적값을 도출해냅니다!
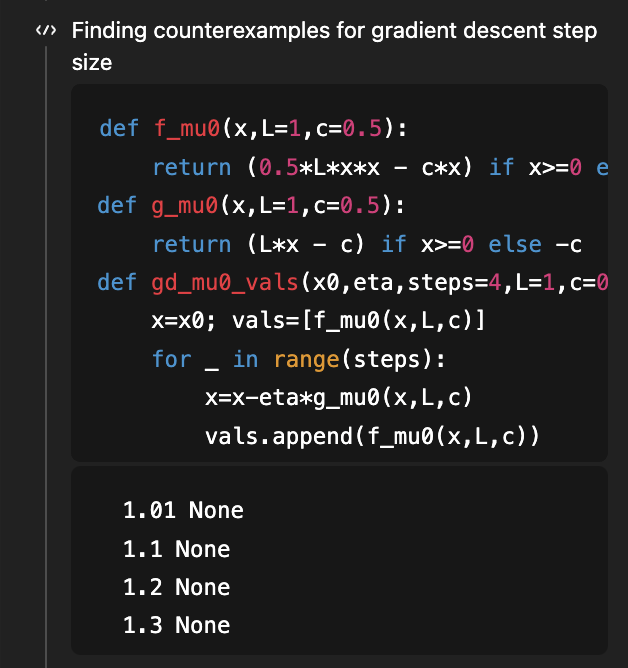
기억하시겠지만, 이 문제는 제가 GPT-5의 연구 능력을 보여주기 위해 처음 사용했던 문제였고, 목표는 매끄러운 볼록 최적화를 위한 경사 하강법이 학습 곡선 자체를 볼록하게 만드는 스텝 크기 조건을 찾는 것이었습니다! eta < 1/L이면 충분조건이고 eta < 1.75/L이면 필요조건이라는 것을 보여주는 좋은 논문이 있었는데, 그 논문의 v2에서는 1.75/L이 올바른 "필요조건"이라는 것을 밝혀내면서 그 간극을 메웠습니다. 지난 8월(4개월 전!), 해당 논문의 v1 버전을 기준으로 했을 때 GPT-5는 충분조건을 1/L에서 1.5/L로 개선할 수 있었습니다(최적값인 1.75/L에는 미치지 못했지만요). GPT-5.2는 아무런 정보도 없이 1.75/L의 필요조건과 충분조건을 모두 도출해냅니다! 필요조건을 도출하기 위해 반례를 탐색하는 코드를 사용합니다. (물론 해당 논문은 여전히 지식 수준 5.2를 넘어서는 수준입니다.)
이 문제는 학습 곡선의 형태를 이해하는 더 넓은 맥락에 속합니다. 이러한 형태의 가장 기본적인 속성은 바라건대 감소한다는 것입니다! 특히 통계적 관점에서, 데이터를 추가한다고 가정했을 때 테스트 손실이 더 낮아진다는 것을 증명할 수 있습니까? 놀랍게도 이는 상당히 직관적이지 않으며 반례도 많습니다. 이 주제는 고전 서적 [Devroye, Gyorfi, Lugosi, 1996]에서 자세히 논의되었습니다(제가 20년 전에 탐독했던 기억이 나지만, 그건 다른 이야기입니다!). 최근 2019년 COLT 공개 문제에서 이 질문의 매우 기본적인 버전들이 여전히 미해결 상태라는 점이 지적되었습니다. 예를 들어, 알려지지 않은 가우시안 분포의 (공)분산을 추정할 때, 위험도가 단조적인가(즉, 데이터를 추가할수록 공분산을 더 잘 추정할 수 있는가)와 같은 질문입니다. @MarkSellke가 GPT-5.2에 이 질문을 던졌고... GPT-5.2가 답을 찾았습니다! 그리고 Mark는 (수학적 지식은 전혀 투입하지 않고 좋은 질문만 던지면서) 모델과 끊임없이 상호작용하며 결과를 일반화해 나갔고, 결국 이 연구는 훌륭한 논문으로 발전했습니다. 이 논문에는 순방향 KL 분류에 대한 가우시안 분포와 감마 분포, 그리고 역방향 KL 분류에 대한 보다 일반적인 지수족 분포에 대한 결과가 담겨 있습니다. 자세한 내용은 다음 링크에서 확인하실 수 있습니다: https://t.co/XLETMtURcd