벤치마크 수치에서 신호를 얻는 것이 점점 더 어려워지고 있습니다. 평균보다는 (가까운) 미래에는 "argmax"도 중요해질 거라고 생각합니다. 모델이 낼 수 있는 최고의 출력값은 무엇일까요? PvsNP 문제를 10번 중 10번 풀 필요는 없잖아요. 한 번이면 충분하잖아요 😅. 이 점을 염두에 두고 제가 본 것 중 가장 인상적인 LLM 출력값에 대해 좀 더 자세히 말씀드리겠습니다.
여러분 중 많은 분들이 선호 애착 모델(바라바시-알베르라고도 함)에 익숙하실 겁니다. 이는 성장하는 무작위 그래프 프로세스로, 각각의 새로운 노드가 기존 노드에 연결될 확률은 노드의 차수에 비례합니다. 이는 X와 같은 네트워크가 성장하는 방식(인기 계정이 더 많은 팔로워를 유치하는 방식)과 매우 유사합니다. (이고르 코르트켐스키의 아름다운 GIF)
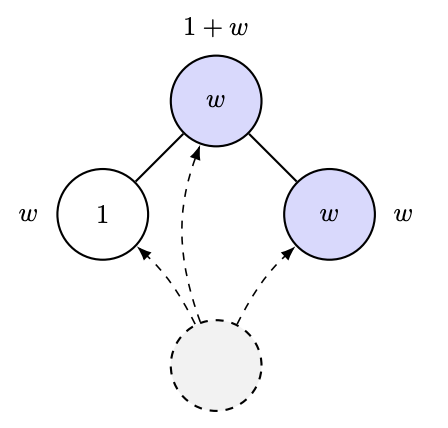
2012년, Ramon과 Comendant는 COLT 개방형 문제에서 선호적 애착 과정의 변형을 제시했습니다. 각 노드는 1 또는 W>1의 "매력도" 매개변수를 가지고 태어나고, 이전 노드와의 연결은 이웃 노드들의 총 매력도에 비례합니다! 즉, 매력적인 친구가 많으면 더 많은 연결을 끌어들이게 된다는 것입니다. 마치 AI 연구실이 성장하는 방식을 시뮬레이션하는 것 같기도 하고요. 🤣. 그들이 던진 아주 간단한 질문은 "그래프를 관찰하여 W를 추정할 수 있는가?"였습니다. [실제로는 이보다 더 정량적인 질문을 던졌지만, 그것이 바로 질문의 핵심입니다.]
당연히 "가장 인기 있는 노드의 성장은 W 같은 것, 즉 차수 통계량에 따라 달라질 수도 있겠구나"와 같은 추측을 하게 될지도 모릅니다. 하지만 적어도 만약 이것이 사실이라면, Ben-Hamou와 Velona의 최근 논문에 따르면 밀접하게 연관된 모델(선호적 애착 대신 균일한 애착을 보이고, 그 변화가 더 높은 확률로 자신의 유인도 수준에 애착하는 것에 기반함)에서 차수 통계량은 그 차이를 구분할 수 없다는 것을 보여주기 때문에, 이는 상당히 미묘할 것입니다! https://t.co/pdwr86OK5A
이제 마침내 제가 지금까지 본 것 중 가장 인상적인 LLM 출력을 말할 수 있습니다. GPT-5는 위에서 설명한 프로세스에서 잎의 한계 분율에 대한 닫힌 형식을 제공하는 다음 정리를 증명했으며 이를 통해 이러한 그래프의 관찰에서 W를 추정할 수 있습니다.
증명(100% GPT-5)은 로빈스 먼로(즉, SGD!) 유형 분석을 사용하여 주요 양의 수렴을 제어하는 놀랍도록 기발한 방법입니다. 또한 증명을 검토하기 전에 GPT-5에 시뮬레이션을 실행하여 공식이 믿을 만한지 경험적으로 확인해 보도록 요청했습니다.
이런 증명을 생각해 내고, 시뮬레이션을 돌리고, 그 모든 과정을 예전에는 한 달 정도 걸렸습니다. 하지만 지금은 오후 한 시간 만에 끝낼 수 있게 되었습니다. 관심 있는 분들은 https://t.co/IfotVApR3X의 4장 4절에서 전체 증명과 자세한 내용을 확인하실 수 있습니다. 추수감사절 잘 보내세요!