GPT 5.2 は、これまでで最高の科学モデルです: GPQA 92.4%、Frontier Math 40%、ARC-AGI-2 52.9%、CharXiv 89% (ツールを含む)、HLE 45% (ツールを含む)... さらに、研究レベルでは、このモデルの信頼性は大幅に向上しました。凸最適化問題を一発で最適値に導出できるようになりました。
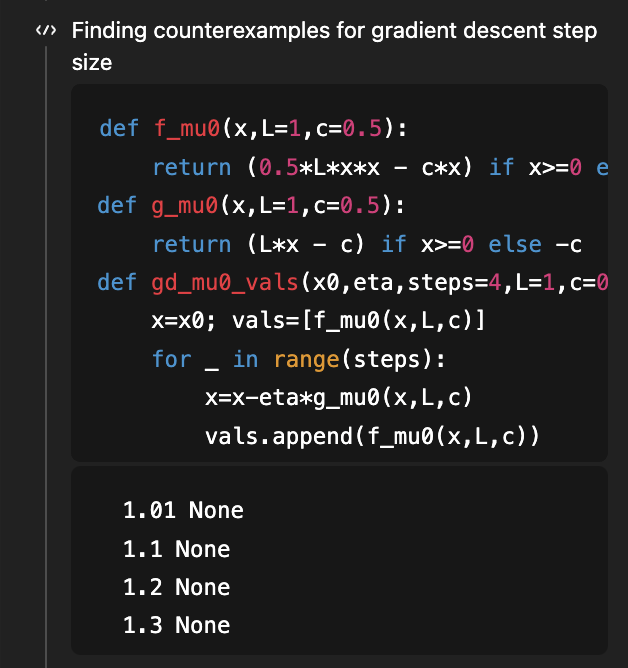
ご記憶にあるかと思いますが、これは私がGPT-5の研究能力を示すために使用した最初の問題であり、滑らかな凸最適化のための勾配降下法が凸状の学習曲線を許容するステップサイズ条件を決定することが目標でした。eta < 1/Lで十分であり、eta < 1.75/Lが必要であることを示す優れた論文があり、その論文のバージョン2では、1.75/Lが適切な「if and only if」条件であることが示され、ギャップが埋められました。 8月(4か月前!)に論文のv1を文脈に当てはめてみると、GPT-5は十分な条件を1/Lから1.5/L(最適な1.75/Lには達していません)に改善することができました。 GPT-5.2は、何も与えられていない状態で、1.75/Lの必要条件と十分条件の両方を導出します。必要な部分を導出するために、反例を検索するコードを使用しています… (そしてもちろん、対応する論文は依然として知識カットオフ 5.2 を超えています)
この問題は、学習曲線の形状を理解するというより広い文脈に当てはまります。このような形状の最も基本的な特性は、おそらく…減少傾向にあるということです!具体的には統計的な観点から、データを追加した場合、テスト損失が減少することを証明できますか? 驚くべきことに、これは全く自明ではなく、多くの反例があります。この点については、古典的な書籍[Devroye, Gyorfi, Lugosi, 1996]で詳しく議論されています(20年前に貪るように読んだのを覚えていますが、それはまた別の話です!)。最近では、2019年のCOLT Open Problemにおいて、この問題の非常に基本的なバージョンが未解決であることが指摘されました。例えば、「未知のガウス分布の(共)分散を推定する場合、リスクは単調か(つまり、データを追加することで共分散をより正確に推定できるのか)?」といった問題です。 @MarkSellkeさんがこの質問をGPT-5.2に投げかけたところ…なんと解決しました!その後、Markさんはモデルと何度もやり取りして結果を一般化し続けました(Markさんからの数学的インプットは特になく、良い質問をするだけです)。そして、この作業はどんどん進みました…最終的に、順方向KLのガウス分布とガンマ分布、そして逆方向KLのより一般的な指数分布族の結果を含む、素晴らしい論文になりました。詳細はこちらをご覧ください:https://t.co/XLETMtURcd