Permettez-moi d'être franc, comme on dit. Je pense que beaucoup de gens adhèrent à une version excessive de cet argument. Mais je crois qu'il existe de nombreuses autres versions qui sont fondamentalement justes.
Que signifie « générer des connaissances », par exemple à propos d'une proposition P vraie mais inconnue ? Je pense que cela signifie qu'il existe une proposition de contexte C qui induit du modèle linéaire un « argument » A vrai qui implique P. Si tel est le cas, alors on a généré des connaissances sur P.
L'affirmation la plus manifestement erronée de cet argument est que cela est impossible. Or, c'est tout à fait possible et même fréquent, souvent de manière assez triviale. Le code implémentant une fonctionnalité de mon application m'est inconnu. Je le demande au LLM. Il me fournit le code. Et voilà, une nouvelle connaissance !
Ceci étant dit, entrons dans le vif du sujet. Tout d'abord, un point fondamental : les connaissances acquises par un LLM sont statiques à court terme. Elles s'effacent entre les sessions. Une fois la notion A acquise, la notion P n'est pas automatiquement « connue ». Cela diffère légèrement du fonctionnement humain.
Une fois qu'Euclide a démontré I.46 : « On peut construire un carré », I.46 intègre son savoir et il peut l'appliquer pour démontrer le théorème de Pythagore. Une fois que le LLM a démontré P, P ne devient pas « une partie de son savoir » de la même manière.
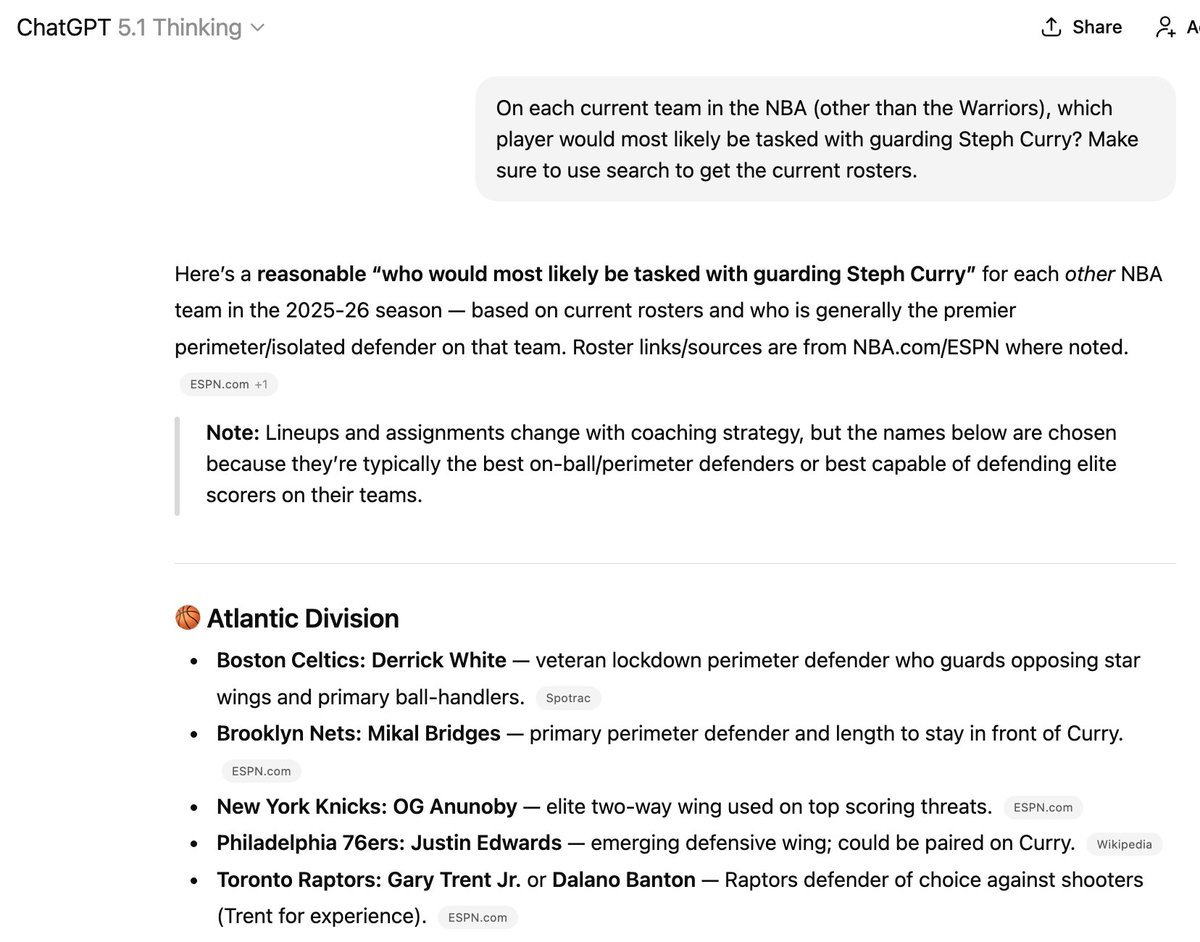
Il existe des méthodes pour tenter d'intégrer P à ses données d'entraînement, mais cela reste très aléatoire. C'est pourquoi ce genre de problème survient. Trois des six joueurs mentionnés ici ne font plus partie des équipes indiquées, mais il est difficile de lui faire « apprendre » de nouvelles choses !
(Au passage, je ne recommanderais pas d'engager cette chose pour entraîner votre équipe NBA.)
Ce point corrobore l'idée selon laquelle « il ne peut combiner que des informations déjà découvertes ». Il connaît ses connaissances actuelles, qui restent globalement stables à court terme (entre deux entraînements) et évoluent de manière imprévisible à long terme.
Je pense que ce point est important concernant les affirmations sur la guérison du cancer et autres. Guérir le cancer ne sera pas comme résoudre un problème de Putnam. Cela impliquera de recenser et de relier de nouveaux faits encore inconnus, et qui pourraient même contredire les croyances actuelles.
D'une certaine manière, je pense que cela ressemblera à la tâche de suivre quel joueur fait actuellement partie de quelle équipe de basketball, une tâche pour laquelle même les modèles de raisonnement les plus sophistiqués, dotés d'un accès internet illimité, restent désespérés à ce jour.
D'accord, une autre piste de réflexion. Le modèle LLM ne génère pas A de manière déterministe. Il génère A avec une certaine probabilité. Avec une autre probabilité, il peut générer B (pour « argument erroné »), ce qui implique une probabilité non nulle. Et nous ignorons quelles sont ces probabilités.
Que dois-je en conclure ? Dans le cas où il a donné la bonne réponse, a-t-il « généré des connaissances » ? Ici, il mélange et remixe divers fragments d’informations mathématiques, un peu comme le décrit le tweet cité que je suis en train de corriger.
Par divers moyens, certains plus manuels et d'autres plus automatisés, je peux vérifier la validité de ces arguments et la véracité de leurs conclusions. Ce faisant, je découvrirai probablement des arguments corrects et des conclusions justes qui seraient jusqu'alors inconnus.
À mon sens, il s'agit moins d'un processus de « génération » autonome de connaissances que d'un processus d'« extraction » de connaissances. Le LLM contient un certain nombre de vérités et un certain nombre d'erreurs. Le défi consiste à extraire les vérités et à laisser de côté les erreurs.
Contrairement à beaucoup d'autres adeptes de LLM, je pense que l'autocomplétion améliorée, la devinette aléatoire du prochain jeton, est en fait la manière la plus juste et la plus utile d'appréhender ces concepts. Je dis cela en tant que passionné de LLM de longue date. Je pense que beaucoup de gens contestent cette caractérisation.
L'idée de base était qu'on ne pourrait jamais rien apprendre de nouveau en devinant aléatoirement le prochain jeton. Mais bien sûr que si ! Si vous laissez tomber un tas d'aiguilles de même longueur sur un parquet, vous pouvez compter les intersections pour estimer la valeur de π. Il y a une multitude d'informations à extraire de cela.
Des processus aléatoires, si on sait comment faire. Mais je me demande bien ce qu'il y a réellement là-dedans. Peut-être que le remède contre le cancer s'y trouve, et qu'il suffit de fournir la bonne invite. Ou alors, il y a peut-être quelques problèmes Erdos non résolus et d'autres choses faciles à résoudre, et c'est tout.