Il devient de plus en plus difficile d'interpréter les résultats des benchmarks. Plutôt que de se fier aux moyennes, je pense que dans un avenir proche, on s'intéressera aussi à l'« argmax » : quel est le meilleur résultat qu'un modèle puisse fournir ? Après tout, il n'est pas nécessaire de résoudre PvsNP 10 fois sur 10, une seule fois suffit 😅. C'est pourquoi je vais vous parler un peu plus du résultat LLM le plus impressionnant que j'aie jamais vu.
Vous êtes probablement nombreux à connaître le modèle d'attachement préférentiel (également appelé Barabási-Albert), qui décrit un processus de croissance aléatoire sur un graphe, où chaque nouveau nœud s'attache à un nœud existant avec une probabilité proportionnelle à son degré. Ce mécanisme est très similaire à la croissance d'un réseau comme X (les comptes populaires attirent de plus en plus d'abonnés). (Magnifique GIF d'Igor Kortchemski)
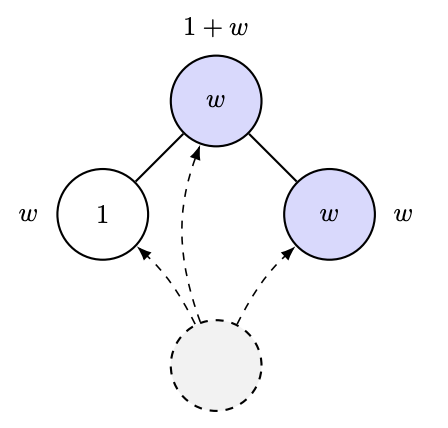
En 2012, Ramon et Comendant ont introduit, dans leur problème ouvert COLT, une variante du processus d'attachement préférentiel. Chaque nœud est doté d'un paramètre d'« attractivité », soit 1, soit W > 1, et la connexion à un nœud précédent est désormais proportionnelle à l'attractivité totale de ses voisins ! Autrement dit, si vous avez beaucoup d'amis attractifs, vous attirerez davantage de connexions. J'imagine que cela simule la croissance d'un laboratoire de recherche en IA, ou quelque chose du genre 🤣. Leur question, très simple, était : peut-on estimer W en observant le graphe ? [En réalité, leur question était plus quantitative, mais l'essentiel en ressort.]
On pourrait être tenté de supposer que la croissance du nœud le plus populaire dépendrait de W, par exemple d'une statistique de degré. Or, si cela s'avérait vrai, ce serait pour le moins délicat. En effet, une étude récente de Ben-Hamou et Velona montre que, dans un modèle très proche (attachement uniforme au lieu d'attachement préférentiel, la variation reposant sur une probabilité plus élevée de s'attacher à son propre niveau d'attractivité), les statistiques de degré sont incapables de faire la différence ! https://t.co/pdwr86OK5A
Je peux enfin exposer ce qui est, à mon avis, le résultat LLM le plus impressionnant que j'aie jamais vu : GPT-5 a démontré le théorème suivant, qui fournit une expression analytique de la fraction limite de feuilles dans le processus décrit ci-dessus, permettant ainsi d'estimer W à partir de l'observation d'un tel graphe.
La démonstration (100 % GPT-5) est étonnamment ingénieuse, utilisant une analyse de type Robbins-Monro (c'est-à-dire SGD !) pour contrôler la convergence des quantités clés. Avant même d'examiner la démonstration, nous avons demandé à GPT-5 d'effectuer une simulation et de vérifier empiriquement la crédibilité de la formule.
Élaborer une telle démonstration, effectuer la simulation, etc., me prenait auparavant environ un mois. Maintenant, cela a été fait en un après-midi. Pour ceux que cela intéresse, vous pouvez trouver la preuve complète et plus de déarxiv.org/abs/2511.16072IV, section 4 de https://t.co/IfotVApR3X. Joyeux Thanksgiving !