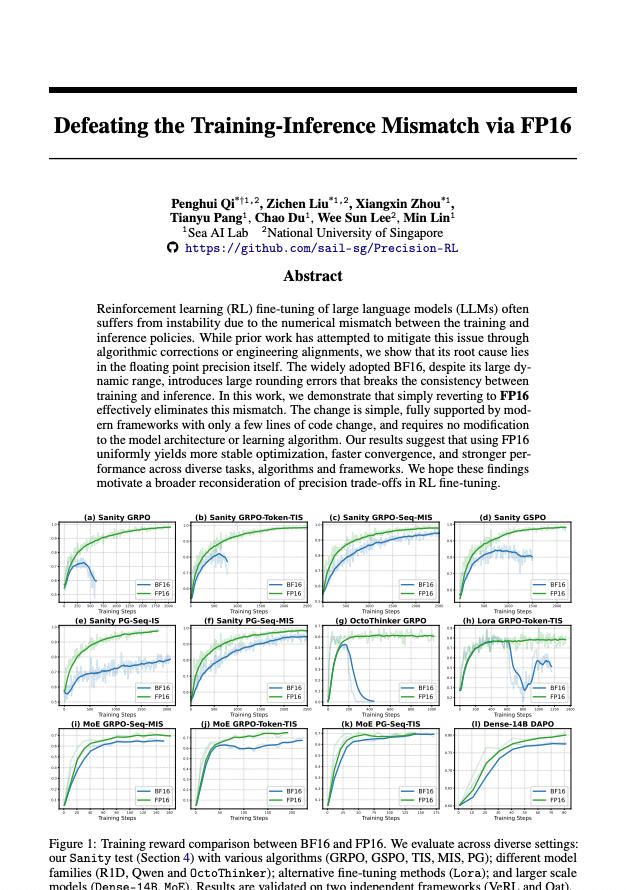
#8 - Surmonter le décalage entre l'entraînement et l'inférence grâce à FP16 Liarxiv.org/abs/2510.26788w36nc Pour continuer sur le même sujet que dans les sections 6 et 7, considérez ceci comme une lecture obligatoire pour vous mettre à jour sur la discussion concernant ce sujet. Les travaux précédents ont tenté de résoudre ce problème de décalage entre l'entraînement et l'inférence par des astuces d'échantillonnage d'importance ou par une ingénierie lourde visant à mieux aligner les noyaux. Cela aide en partie, mais : >nécessite des ressources de calcul supplémentaires (passes avant supplémentaires) Cela ne résout pas vraiment le problème d'optimiser l'un et d'en déployer un autre. peut encore être instable La thèse de cet article est donc la suivante : le véritable méchant est BF16. Utilisez FP16. Je me suis bien amusé à créer plusieurs mèmes à ce sujet sur mon compte Twitter.
#9 - Le potentiel de l'optimisation du second ordre pour les LLM : une étude avec la méthode de Gauss-Newton comarxiv.org/abs/2510.09378.co/wlkpXHz4sf L'article montre que si vous utilisez la courbure de Gauss-Newton réelle au lieu des approximations simplifiées que tout le monde utilise, vous pouvez entraîner les LLM beaucoup plus rapidement : la méthode GN complète réduit le nombre d'étapes d'entraînement d'environ 5,4× par rapport à SOAP et de 16× par rapport à muon. Ils ne fournissent aucune garantie théorique concernant cette affirmation et celle-ci n'a pas été testée à grande échelle (seulement 150 millions de paramètres).