GPT 5.2 es nuestro mejor modelo para la ciencia hasta el momento: 92,4% GPQA, 40% Frontier Math, 52,9% ARC-AGI-2, 89% CharXiv (con herramientas), HLE 45% (con herramientas)... Además, a nivel de investigación, el modelo se ha vuelto mucho más fiable. ¡Ahora resuelve el problema de optimización convexa de una sola vez hasta su valor óptimo!
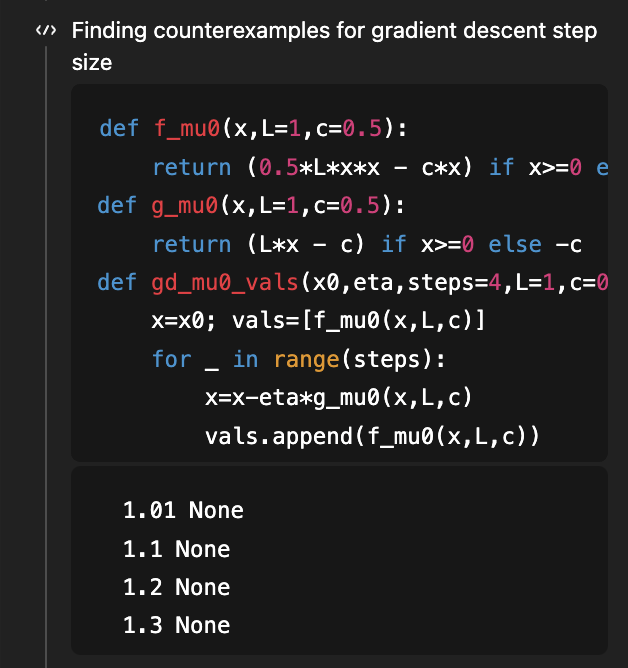
Si recuerdan, este fue el primer problema que utilicé para demostrar las capacidades de investigación de GPT-5. El objetivo era determinar la condición de tamaño de paso bajo la cual el descenso de gradiente para la optimización convexa suave admite una curva de aprendizaje que, a su vez, es convexa. Había un buen artículo que demostraba que eta < 1/L es suficiente y eta < 1,75/L es necesario, y una versión 2 de ese artículo cerraba la brecha, demostrando que 1,75/L es la condición correcta "si y solo si". En agosto (¡hace 4 meses!), dada la versión 1 del artículo en contexto, GPT-5 pudo mejorar la condición suficiente de 1/L a 1,5/L (muy por debajo del valor óptimo de 1,75/L). Ahora, GPT-5.2, sin nada, deriva la condición necesaria y suficiente de 1.75/L. Para derivar la parte necesaria, usa código para buscar contraejemplos... (y, por supuesto, el artículo correspondiente todavía está más allá del nivel de conocimiento de 5,2)
Este problema se enmarca en un contexto más amplio: la comprensión de la forma de las curvas de aprendizaje. La propiedad más básica de estas formas es que, con suerte, ¡son decrecientes! Desde una perspectiva estadística específica, suponiendo que se añaden más datos, ¿se puede demostrar que la pérdida de la prueba será menor? Sorprendentemente, esto no es tan obvio y existen numerosos contraejemplos. Esto se analizó extensamente en el libro clásico [Devroye, Gyorfi, Lugosi, 1996] (que recuerdo haber leído con voracidad hace 20 años, ¡pero esa es otra historia!). Más recientemente, en un problema abierto de COLT de 2019, se señaló que algunas versiones extremadamente básicas de esta pregunta aún están abiertas, como: si se estima la (co)varianza de una gaussiana desconocida, ¿es el riesgo monótono (es decir, añadir más datos ayuda a estimar mejor esta covarianza)? @MarkSellke le planteó esta pregunta a GPT-5.2 y... ¡la resolvió! Mark intercambió ideas con el modelo para seguir generalizando el resultado (sin aportación matemática por su parte, salvo por buenas preguntas) y siguió avanzando... finalmente se convirtió en un buen artículo, con resultados para distribuciones gaussianas y gamma para KL directa, y familias exponenciales más generales para KL inversa. Puedes leer más sobre esto aquí: https://t.co/XLETMtURcd.